Toolpath strategies for the layman

Tutorials
1

Trying to work out improvements for this.

AIUI, Carbide Create has the simplest possible toolpath strategy which has some potential problems:

  • plunge along outside edge
  • move at constant speed along perimeter
  • move in by stepover
  • repeat

(I’m considering pockets only to keep this simple)

There’s a bit of a discussion / listing of toolpath strategies at: Complete Guide to CAM Toolpaths and Operations for Milling for reference.

I believe the above technique would fall under “Linear Machining”.

The obvious alternative to the above would be to:

  • plunge at the center
  • spiral outwards from the center
  • repeat

(for a circular pocket — one would need to add a technique for clearing the remaining areas (is there a geometric term for two lines joined by a convex arc?) — I guess arbitrary shapes would require topology which my high school geometry teacher wanted me to study)

I wonder if the above would be improved by:

  • plunge at center to depth per pass
  • spiral out in an upward climbing motion to half the depth per pass
  • do a circle around the perimeter gradually plunging to the depth per pass
  • spiral in to the center (possibly reversing the direction of the cut?)
  • repeat

I’m currently working through developing some OpenSCAD modules which will cut out specific shapes (possibly bounded by a ball-nosed endmill) — next will be writing METAPOST macros which describe the equivalent geometry in 2D, then TPL (Tool Path Language) programs to do the actual toolpaths which I’m considering above.

I’ve been reviewing:

as well as the links at: https://wiki.shapeoko.com/index.php/CAM#Toolpath_strategies

EDIT: and found this a useful overview:

If anyone has any thoughts or further resources to share, I’d be grateful.

EDIT: Researching a bit more I found:

which notes:

To facilitate high speed machining, a CAM system should:

  • Maintain a constant chip load
  • Minimize feed rate losses
  • Maximize program processing speed

and also notes the desirability of curved/circular movement so as to maintain speed and avoid moving into/out of a corner linearly which slows the machine down (interestingly, exiting at a corner is advocated as one strategy to minimize this).

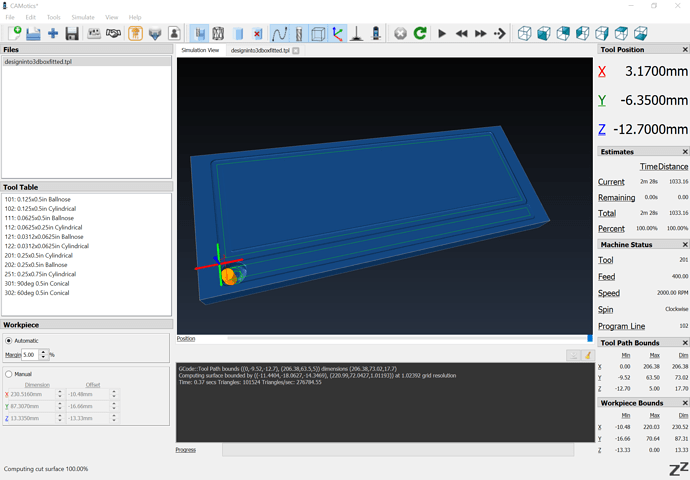
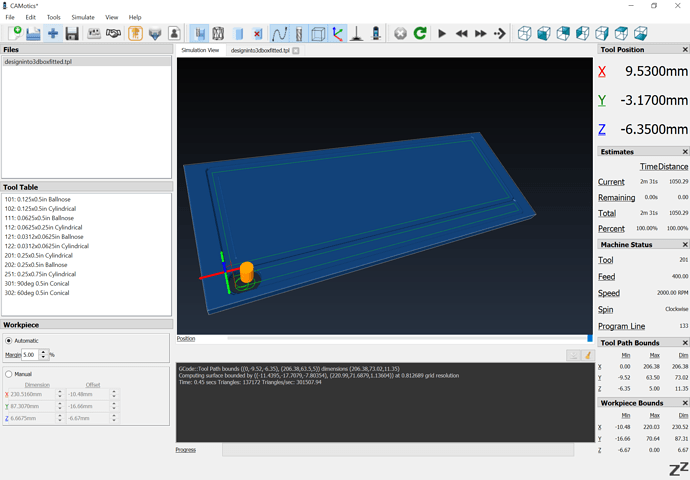
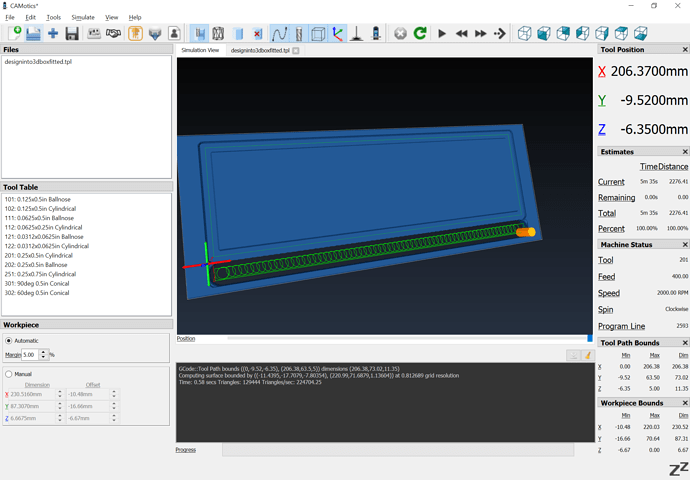
To frame all of this, I found it somewhat difficult to do the machining on a fitted box:

and had to add roughing clearance and finishing passes — I’m hoping to work up an optimal toolpath strategy which doesn’t require being beholden to Autodesk.

EDIT: a different commercial program, but an opensource plug-in mentioned at: Creating a Trochoidal Slot Milling Toolpath - #5 by siemen - Rhino for Windows - McNeel Forum

and further research on GitHub found:

which seems to be a toolpath option for HeeksCNC — the mention of “freesteel” is interesting — I can recall it coming up as a promising development a while back, but on which work was halted (or transferred to some other project?).

and apparently the FreeCAD folks have been working on this, with images which match my understanding as noted above:

https://forum.freecadweb.org/viewtopic.php?t=30127&start=60

and further images are shown at: Blog - NexGenSolutions (odd shape intended to showcase this technique) and https://v4.e-cam.it/article/60-adaptive-toolpath-strategy (a simple triangle).

5 Likes
2

Finally starting in on this in earnest.

First consideration is where to begin — trochoidal toolpaths seem to be most useful for clearing slots, so assuming a slot along the X-axis, twice as wide as the diameter of the endmill, beginning with a helical plunge at that point, and then bottoming out the pocket should be a reasonable beginning.

Before doing that, we have to ensure that all numbers are numbers, see: https://groups.google.com/forum/#!topic/camotics-users/onAh-zOAIv8

With that out of the way, we begin with a move to the starting point:

rapid({x: px+pdiameter, y: py+pdiameter, z: 0});  // Go to start position

and then make a helical plunge (for simplicity we’ll be doing full depth cuts, and not leaving a roughing clearance):

arc(pdiameter/2, 0, -pdepth, 2*Math.PI, XY)

which we then repeat so as to have a flat bottomed pocket:

image
image.png2067×1440 213 KB

1 Like
3

Unfortunately, it’s moving clockwise, and per https://www.researchgate.net/figure/Trochoidal-milling-toolpath-with-circular-model-left-and-true-trochoidal-right_fig1_317057876 it would be better to move counter-clockwise.

Checking the docs https://tplang.org/#arc we find that this is simply a matter of the sign on the rotation unit (radians), so we change to:

arc(pdiameter/2, 0, -pdepth, -2*Math.PI, XY)//helical plunge
arc(pdiameter/2, 0, -pdepth, -2*Math.PI, XY)//flatten bottom

which gets us counter-clockwise.

Since TPL doesn’t afford Bézier curves we will change that last to move through one-fourth of the circle:

arc(pdiameter/2, 0, -pdepth, -2.5*Math.PI, XY)//flatten bottom

and arrive at the lower edge of the pocket, in line for a movement long the bottom edge.

Since the Z in an arc is incremental, the last two need to be changed into:

arc(pdiameter/2, 0, 0, -2.5*Math.PI, XY)//flatten bottom

icut({x: pdiameter/2});  // advance
arc(0, pdiameter/2, 0, -1*Math.PI, XY)//trochoidal cut

which leaves us at:

image
image.png2067×1440 214 KB

swinging around to the position for the next cut using only arcs of a circle smoothly joined together is an interesting effort in geometry:

image
image.png2067×1440 316 KB

1 Like
4

Turning that into a loop:

var i;
for (i = 0; i < pwidth*pdiameter*0.75+1; i++) { 

arc(0, pdiameter/2, 0, -1*Math.PI, XY)//trochoidal cut

arc(0, -pdiameter/4, 0, -0.5*Math.PI, XY)//begin return
arc(pdiameter*0.75, 0, 0, -0.5*Math.PI, XY)//finish return
}

we get:

image
image.png2067×1440 229 KB

For some reason the logic to increment the counter isn’t making sense, hence the weird value for i — hopefully I can puzzle that out presently.

1 Like
5

And after all that I find that TPL doesn’t seem to be generating G2/G3 arcs, but polylines.

Turns out it’s an option:

tplang --linearize=false program.tpl

and will work in a future release.

1 Like
6

Interesting alternative toolpath.

http://www.forgacsolaskutatas.hu/innovacio/can_trochoidal_milling_be_ideal/

1 Like