V bit depth of cut

[Lookin4help (Mark Roberts)]

I am looking for the math formula that will tell me what the depth of cut will be between two vectors using any given V bit. I have seen a YouTube video on this, but it was too far over my head to understand. I guess what I need is the formula and a corresponding example.

Thanks in advance for any help.

[WillAdams (William Adams (Carbide 3D))]

It’s geometry/trigonometry — Pythagoras’ Theorem.

Alternately, just draw the tool in profile and a rectangle of the desired width/thickness.

[Lookin4help (Mark Roberts)]

Will: I know that A squared + B squared = C squared. However, with the problem, as I understand it, I only know B. Sides A and C remain unknown. So, I only know side, B and its opposing angle (1/2 of the V bit in use). There is some calculus in there that can figure that out, but I don’t have that. Bottom line, I’m still lost.

[Stankus (John Stankus)]

If I understand what you are asking for is: For a feature of a particular width what depth do I need to use for a particular angle V-bit? If that is correct the formula you want should be

But since this should give a constant ratio between depth and width for each particular angle v-bit here is the calculation:

V bit angle	Multiply Width of cut by this number to get depth
5	11.452
10	5.715
15	3.798
20	2.836
25	2.255
30	1.866
35	1.586
40	1.374
45	1.207
50	1.072
55	0.960
60	0.866
65	0.785
70	0.714
75	0.652
80	0.596
85	0.546
90	0.500
95	0.458
100	0.420
105	0.384
110	0.350
115	0.319
120	0.289

John

[WillAdams (William Adams (Carbide 3D))]

Specifically, you know two values:

• diameter to which you wish to cut
• V angle

I always look this sort of thing up at:

Right Triangle Calculator with steps

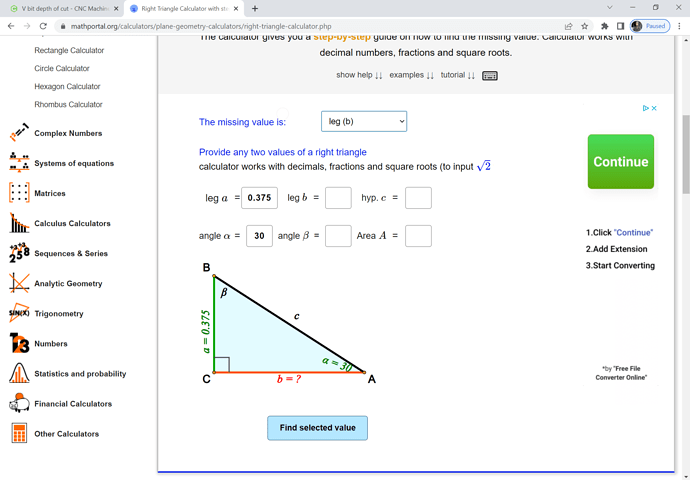
so assume the V endmill is on its side, and half its angle equals angle alpha and the dimension a == half the width which we wish to cut to, so we are trying to determine length b — given for an example:

• 60 degree V endmill
• cutting to a width of 0.75"

We need to enter the values:

• alpha == 30 degrees
• a == 0.375"

and

b == 3/8" / tan(30 degrees)

tan of 30 degrees == 0.577350269

so we EDIT: correction divide (not multiply):

3/8" / 0.577350269

to get:

0.649519053

for the depth which we need to cut to.

For an example of drawing things up in profile and just setting the depth thus see

45° angled cut?

I’m using carbide create pro and shapeoko 4. I truly dont understand the 3d modeling aspect of the program at all and this is probably a simple cut but I can’t seem to figure it out. The material is 1/2 inch thick and I want to cut the edge at a 45° angle. I have a 1/4 inch vee bit. Could anyone point me towards a resource that would explain this to me? [20221106_181237]

[neilferreri (Neil Ferreri Ω)]

@WillAdams

so we multiply:

3/8" * 0.577350269

to get:

0.952350269

I think you want to divide here.

Width of cut / 2 / tan(half angle of bit)

Here’s a post I wrote explaining the math, but looking for the width. We just change the equation.

Vee bit cutting accuracy issues

No, I thought your design had the depth of cut at 0.478". The effective diameter of the V-bit at that depth would be 0.396". You would enter a bit diameter of 0.396". The explanation… Here’s a 45deg bit: [bit] A cross-section is just two right triangles with the cut angle at 22.5 degrees: [cutaway] Depending on the depth of cut, the effective cut radius would change: [cutDepth] If you remember SOHCAHTOA from high school math, you would eventually get to that side of the triangle would …

[Lookin4help (Mark Roberts)]

John: That’s not quite what I asked . . . I think. Maybe an example would be better. So, if I have two vectors that are .05 inches apart, and I have a 90 degree V bit, what is the dept to which the V bit will carve.

[Dooryard (Steven Knox)]

I’m very certain those replies are what you’re looking for. Using Stankus table (I’m saving that) I’m able to confirm Wills example. they both give the same values. 0.05" gap is not a lot and a 90deg vbit will not cut very deep between them. What is the end result you’re looking for? because with those conditions you’ll have a very shallow 0.025" deep carve.

[Stankus (John Stankus)]

(A quick edit since I was off by a factor of two)
So are your running along each vector with the v-bit and wanting to know how high the ridge is between them? Two parallel v-bit paths with make a W shape with the middle of the W’s height dependent on the spacing (this height can be calculated from the bottom of the W easiest).
It would use the calculations I provided. Take the spacing between the two vectors.and multiply by the factor in my previous post. That should give you the height of the ridge relative to the BOTTOM of the v-bit groove. For your example of 0.05 inch spacing and a 90 deg v-bit. The factor above for a 90 deg v-bit is 0.500, so the height of the ridge between the v-bit valleys is 0.05” X0.500 which should be 0.025”

General form (contingent of cut being deep enough for the tool paths to intersect)
Height of ridge=(spacing) X (V-bit factor)

If that isn’t what you are asking, a picture might help.

John

[Lookin4help (Mark Roberts)]

Will: That’s what I was looking for. Thanks.

[Lookin4help (Mark Roberts)]

John: My apologies. You were right and I was wrong. The value your table supplies is the same results that Will’s web page shows. I do have a followup. I’m not the greatest math guy and I tried to write a formula in Excel using what you supplied. The formula looks like: =B6/2*TAN((B7/2)) where B6 is width or distance between two vectors, and B7 is the angle of the V bit. When I input .05 in B6 (width between two vectors) and 90 for the value in B7, the angle of the V bit, the result I get is .040494, but according the web page and your calculations it should be .05. There must be an error in my formula and am wondering if you can spot it?

Thanks

[Stankus (John Stankus)]

(edit cause there is one more issue here)
Just an order of operations issue.
Try =b6/(2*tan(b7/2))

The excel trig functions use radians for the angle, so if using degrees the formula would be
=b6/(2tan(b7pi()/360))

My initial answer did not do the conversion from degrees to radians

John

[neilferreri (Neil Ferreri Ω)]

Or…
=B6/2/TAN((B7/2))

[Tod1d (Tod (with 1 'd'))]

@neilferreri

=B6/2/TAN((B7/2))

This one actually works… =(B6/2)*TAN(RADIANS(B7/2))

[neilferreri (Neil Ferreri Ω)]

@Tod1d

This one actually works… =(B6/2)*TAN(RADIANS(B7/2))

And THIS one works correctly:

=B6/2/TAN(RADIANS(B7/2))

[Stankus (John Stankus)]

weird thing when I edited my prior post to correct the radians the multply sign disappeared in the corrected formula (but not the original version in radians)

[Tod1d (Tod (with 1 'd'))]

@neilferreri

And THIS one works correctly:

=B6/2/TAN(RADIANS(B7/2))

Right you are! (Teamwork )

[Lookin4help (Mark Roberts)]

Thank you for the help with the formula. I’m a happy camper now. Blessings to all.