I had a complete derivation of the math for this method written up, but kept hitting a 500 internal server error when trying to post, so I will try a cut down version without the derivation.
I had some issues with holes not being the correct size so I thought I would check the X and Y axis calibrations. The method in the Shapeoko CNC A to Z, has the issue that to eliminate the runout effects you had to measure faces that were facing the same way. This can be challenging to do accurately.
I had the realization that the runout effects are independent of the length of the feature, so if I can accurately measure two different lengths the difference would eliminate these effects.
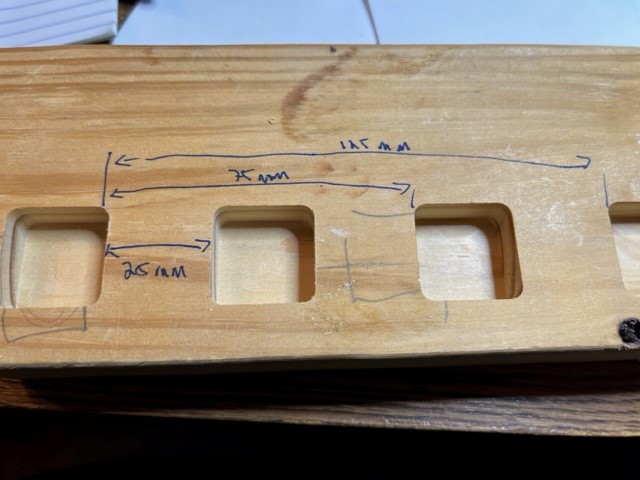
I programmed (in Fusion 360) a series of pockets 25 mm wide spaced 25 mm apart (pocket width is not relevant since the distance between outside walls is what we are measuring) I had a picture of my pattern in the prior attempted post, I will put up as a reply if I can get this post to actually post.
I derived a relationship for the length actually cut, vs what was commanded by the software. In the model, I characterized the error in the steps/mm as a relative factor (effective value = error factor x nominal value). I included an error factor for steps/mm and for tool diameter.
Length(actual) = Length(commanded)/error(steps/mm) + diameter(1/error(steps/mm) - error(diameter))
(it looked prettier in the equation editor I use in my teaching.)
You can see that the error in the tool diameter is not a function of length. So if I measure faces with my caliper at two different lengths, say a nominal 25 mm and nominal 125 mm, the difference will subtract off that part of the error. In my example the difference in the actual measurements of length vs the difference in the commanded lengths will let you calculate the error in the steps/mm setting.
Now to get more sophisticated, you can actually back out the effective tool diameter from this information (runout and over/under sizing)
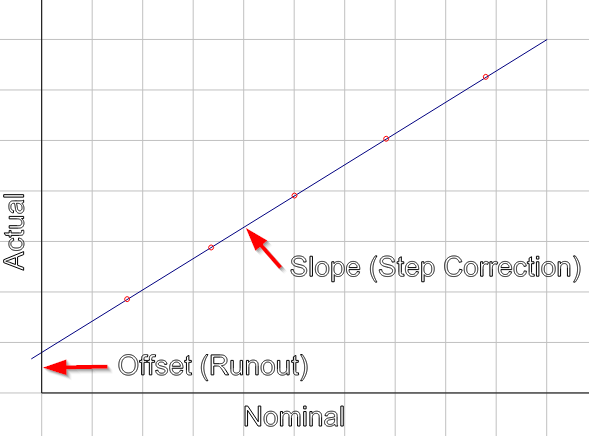
The way to do this is to plot the actual distances vs the commanded distances and fit the line. (easily done in excel).
The slope of the line is m= 1/error(steps/mm). (where the line if y=mx+b)
The intercept is b=diameter (1/error(steps/mm)-error(diameter))
which can give you the error(diameter)
error(diameter)=m-(b/diameter(nominal)
Again the equations were clearer in the equations editor that was not being able to be posted.
Thoughts/comments?
John