Interesting question. And yes, you’re right, you can pick the helix angle to ensure full axial engagement even for a radially narrow cut, so that the cutting forces are essentially constant. Here’s some data:
Forces (Newton) for one revolution for the SECO JH40060, which has a very sharp edge at low helix angle (25 degree):
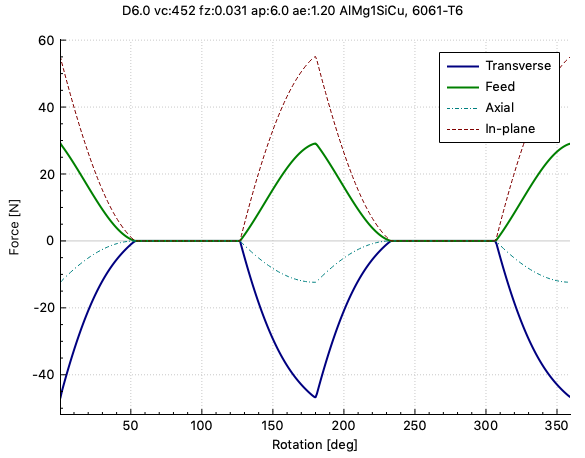
Keeping everything the same, but changing the helix angle to 40 degree:
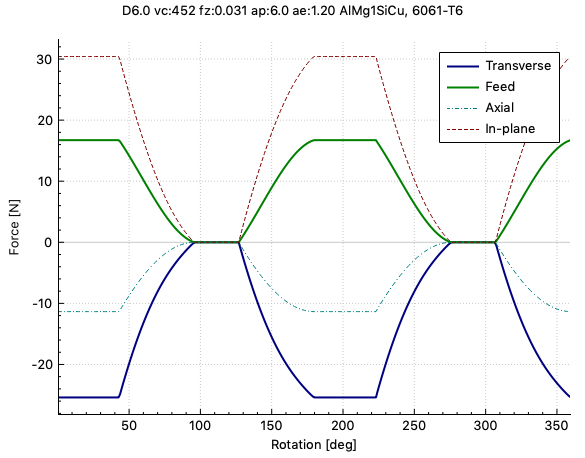
And finally 55 degree:
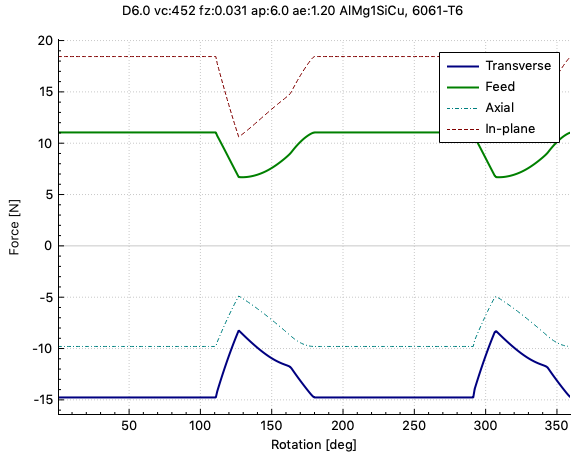
This last would be close to what you suggest, forces practically constant. Iff, and that’s the problem on a Shapeoko, if you can keep the chips from clogging up the flutes (just my impression with higher helix angle endmills).