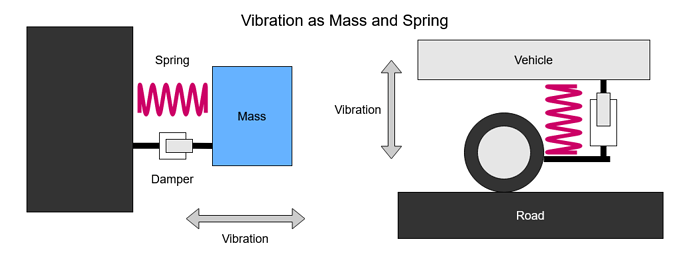
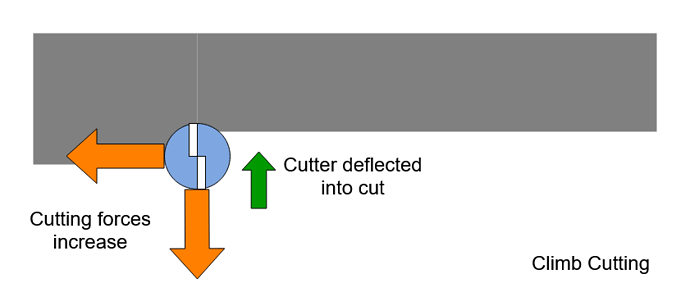
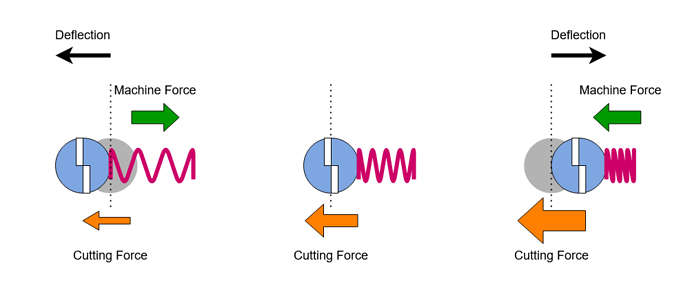
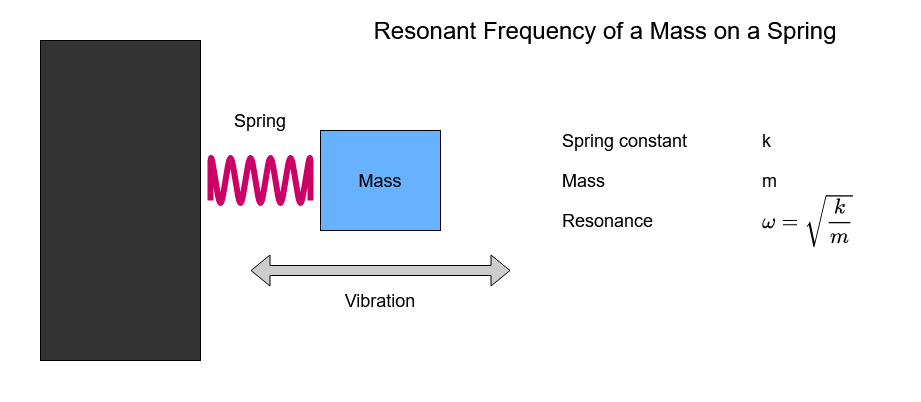
Chapter 3 Deflection Measurements and Model
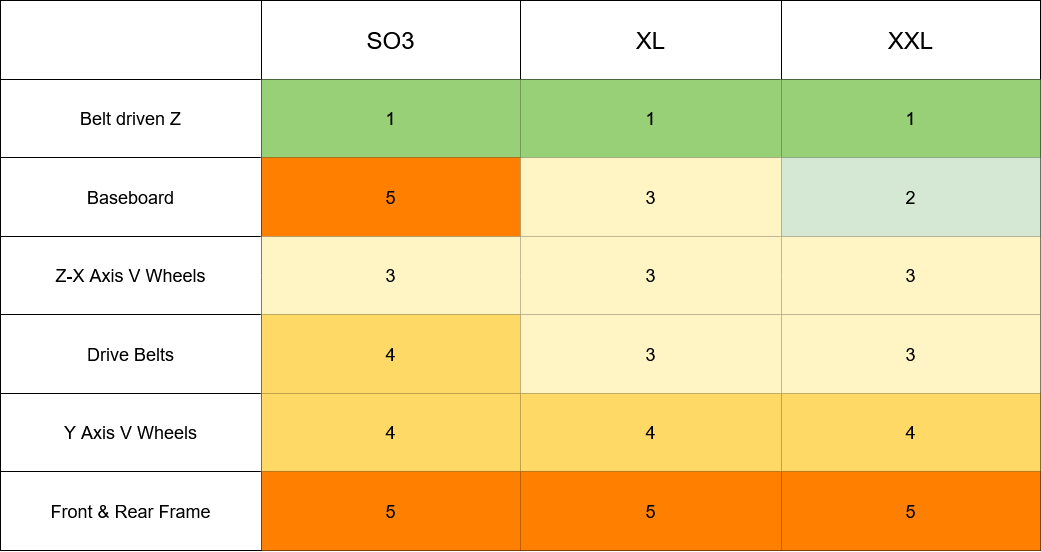
First Suspect – Baseboard
Our first suspect for deflection is the notorious baseboard of the XXL machine.
Starting with the frame, who main purpose is to hold the Y rails square to each other and level above the baseboard. The front and rear metal frames are linked by 3 steel cross-straps. This is then topped and held square by two 18mm MDF sheets.
The frames and steel straps are both folded to provide some rigidity, but this is limited over the width and depth of the XXL.
Calculating the expected deflection for one of the steel straps under a 5kg weight in the centre yields 2.2mm. This is consistent with what I measured on my machine before bolting the baseboard down to something solid.
The most visible issue to most users appears to be sagging of the baseboard over time which results in the spoil-board losing flatness. The underlying cause is the lack of rigidity in the baseboard support straps. If we are concerned with deflection and vibration, holding the workpiece still is a good place to start. Remember that there are vertical forces in cutting as well as horizontal and vertical movement in the workpiece can interact with the nodding mode of Z axis deflection.
SO3 vs XXL
In what is a recurring theme, the SO3 produces a calculated 0.27mm deflection for the same weight vs. the 2.2mm on the XXL. Score one for the Shapoko Pro.
Aluminium Baseboard
As replacing the MDF with a 10mm Aluminium sheet is a popular upgrade, a quick online calculation suggests that for the same 50N load in the centre, even without the steel straps this would only deflect 0.2mm on the XXL and 0.02mm on the SO3.
Second - V Wheels
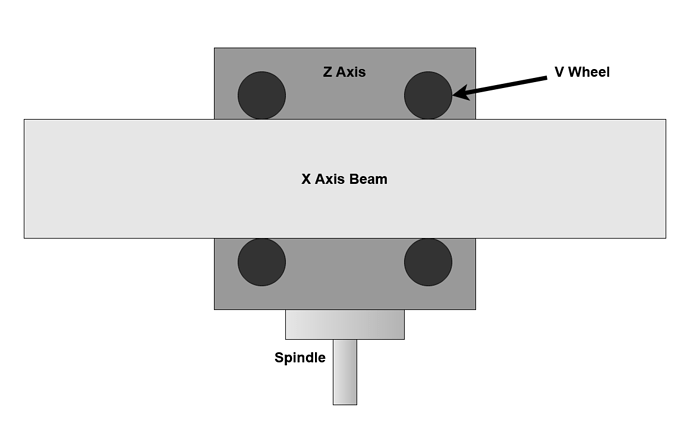
The next significant source of deflection in the machine is the V wheels which allow the linear motion along the X and Y axes. In an ideal world these would be frictionless and only allow movement in one direction, but we don’t live in an ideal world. However good our drive belts are, they can’t make up for the additional movement allowed by the V Wheels or ignore the rolling resistance.
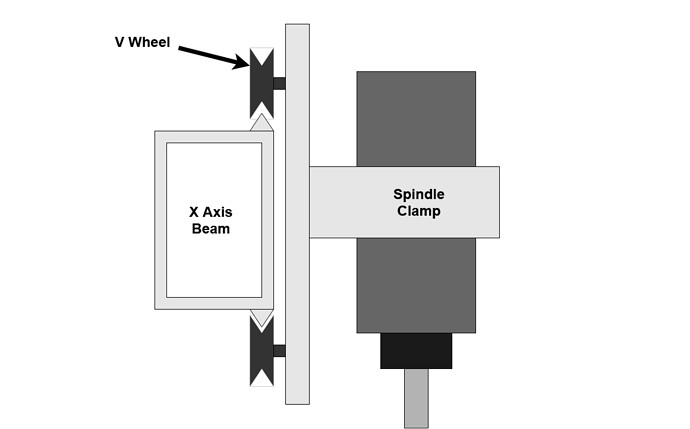
Assuming you already have a Z+ or HDZ, the first set of V Wheels are those mounting the Z carriage to the X axis rail. These are under the greatest stress and are responsible for much of the linear motion deflection.
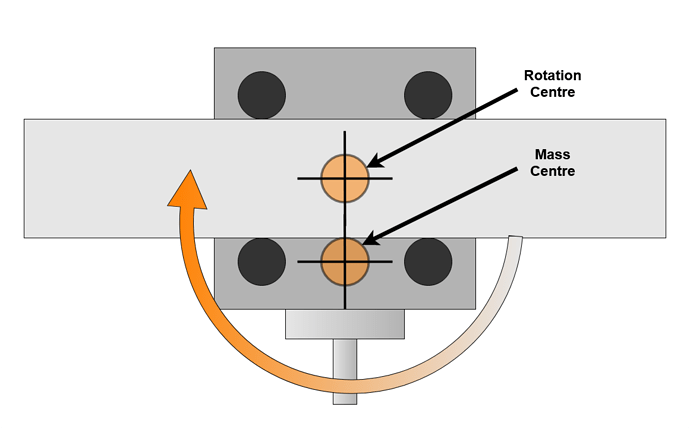
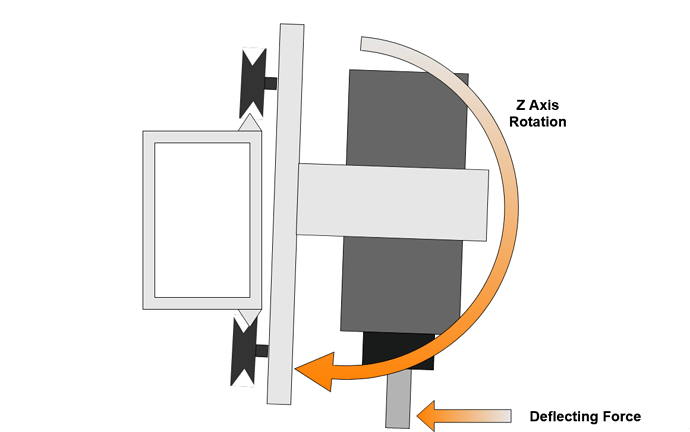
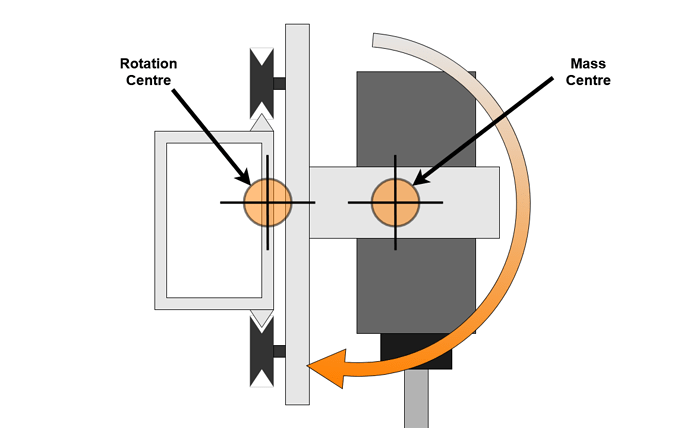
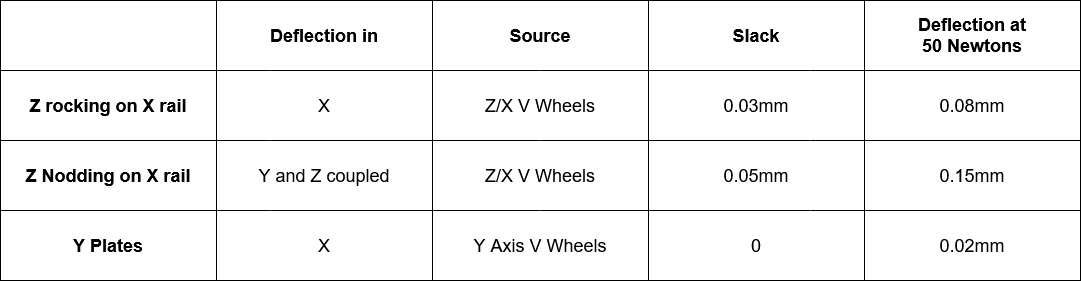
I found two main modes of deflection in the X axis V Wheels, the first is rotation of the Z carriage about the Y axis. This is allowed by radial play in the V Wheels.
When vibrating, this rocking motion only needs to rotate the Z assembly, with the centre of rotation close to the centre of mass which further reduces the ability of the V Wheels to resist. This vibration mode is likely excited by deep cuts traversing along the X axis. The resonance for this mode is rotational and likely higher frequency than the linear belt resonance mode. Consider shaking a can of beans by twisting vs. up and down, although neither case is desirable for the bean.
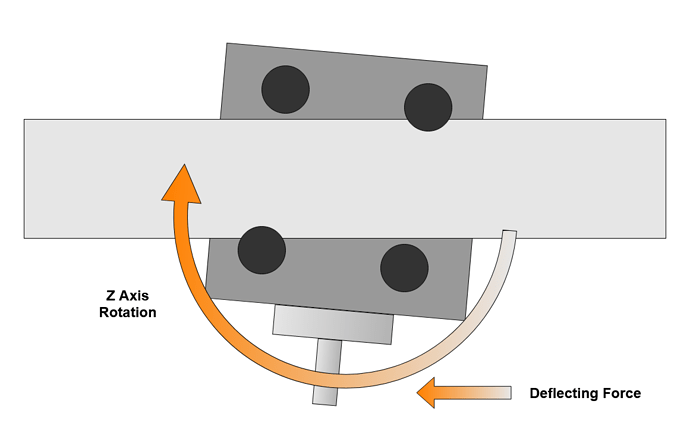
The second is a nodding movement where the Z axis rotates around the X beam, this is allowed by axial play in the V Wheels where they are less effective than in radial. This nodding movement is more displacement than rotation and therefore the spindle and Z mass take more force to move.
This mode is excited by deep cuts moving in X or Y axes and vertical forces generated by the helix on cutters. As this mode changes cutter vertical engagement as well as radial it can be quite violent in terms of cutting force changes and resulting vibration.
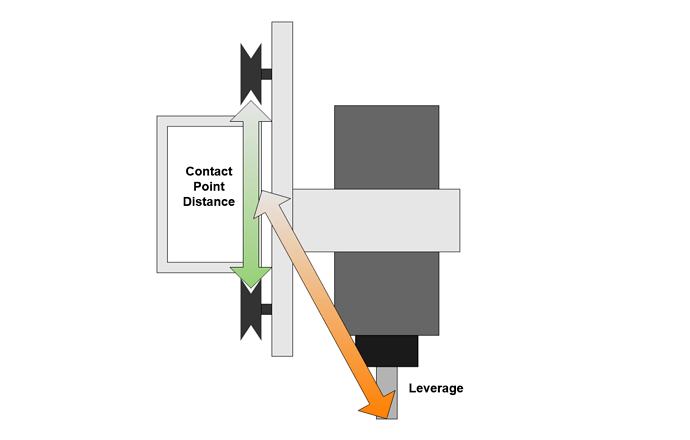
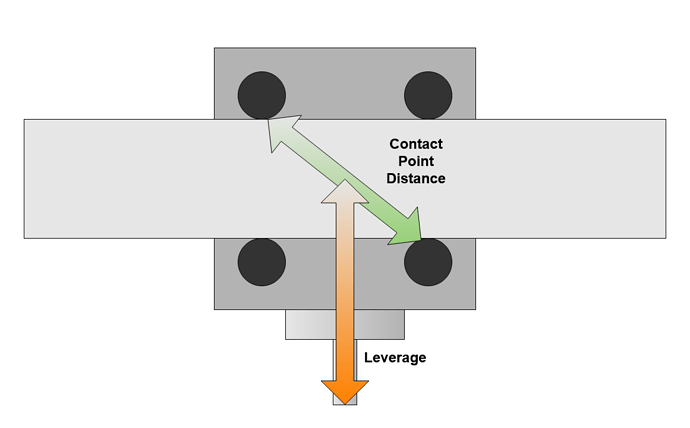
For both of these modes the small spacing of the Z carriage V wheels means that cutting forces are amplified and have high leverage over these wheels. This also suggests that stacking the workpiece up toward the X axis on additional spoilboards, vices or jigs may help reduce some vibration modes.
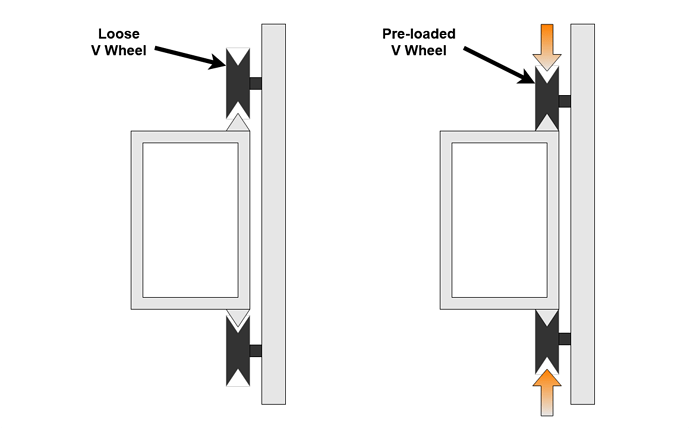
A common response to this unwanted movement, certainly mine initially, was to increase the preload on the V Wheels. This initially ensures that there is no gap and then starts to deform the V Wheel onto the rail making the assembly feel more rigid and increasing the effective spring force of the wheels. One outcome of this is to reduce the deflection for applied cutting forces but this only works up to a point and comes at the cost of increased rolling resistance and eventually lumpy or broken V Wheels.
Y Plates
The second sets of V Wheels are on the Y plates at each end of the X beam. These show much less deflection, 0.02mm for 50 Newtons left / right in X. I think that these wheels contribute less to the overall deflection and vibration for a few reasons;
- There are eight of them not four
- They are spaced further apart and therefore there is less leverage over them
- The additional mass of the X axis beam and steel Y plates
How much deflection?
On my machine at a reasonably high preload
Overall, the V Wheels contribute a major part of the total deflection, even more so on the smaller machines. Increasing preload can reduce deflection a little, but at the expense of early wear-out and increased backlash. I have no recommendation on ‘how tight’ or any sensible way to measure preload.
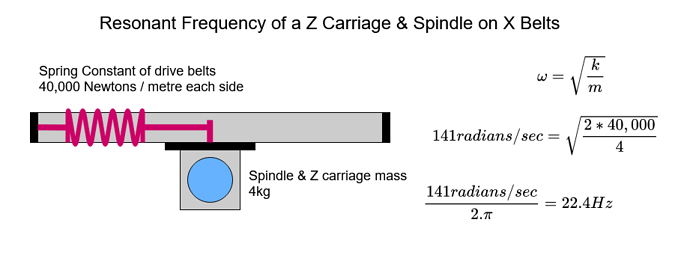
Third - Drive Belts
The Shapeoko drive belts are responsible for a significant part of the overall deflection and, as before, more deflection on the larger machines. In particular, the belt on the X axis is likely to play a significant part in spindle vibration by allowing the Z carriage to move left and right as it stretches. This is in addition to the rotation movement from the V Wheels.
It is useful, therefore, to understand how the drive belts work. To do this, we can produce a simplified model of the belts as used on our machines.
Belt Backlash?
The first element is to find out whether the drive belts exhibit the same, bowling ball in a box, type backlash as a ballscrew, leadscrew or rack and pinion system
(source; Gates belt drive design manual)
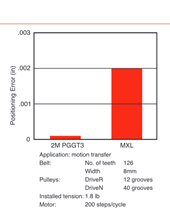
Well, they do, but only a tiny amount. According to the Gates’ data (our belts are the 2M PGGT3 type) around 1 or 2 tenths of a thou (or 0.005mm in sensible units). This is impressive, but then this belt geometry was designed for positioning applications and therefore does absolute position pretty well (assuming you did all your set-screws up properly).
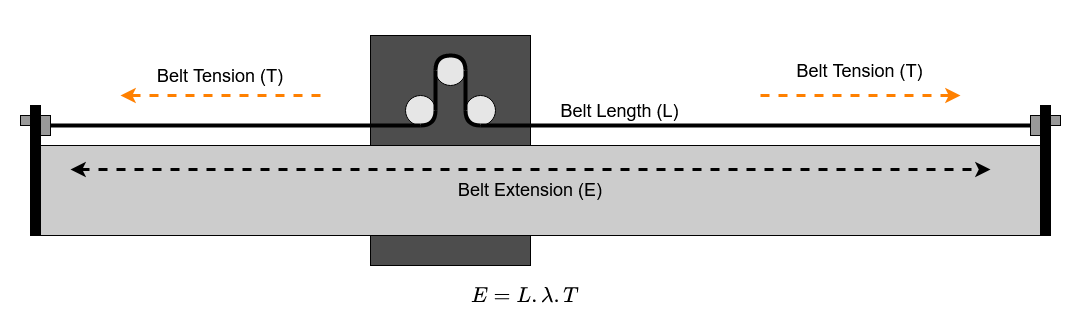
Belt Tension and Extension
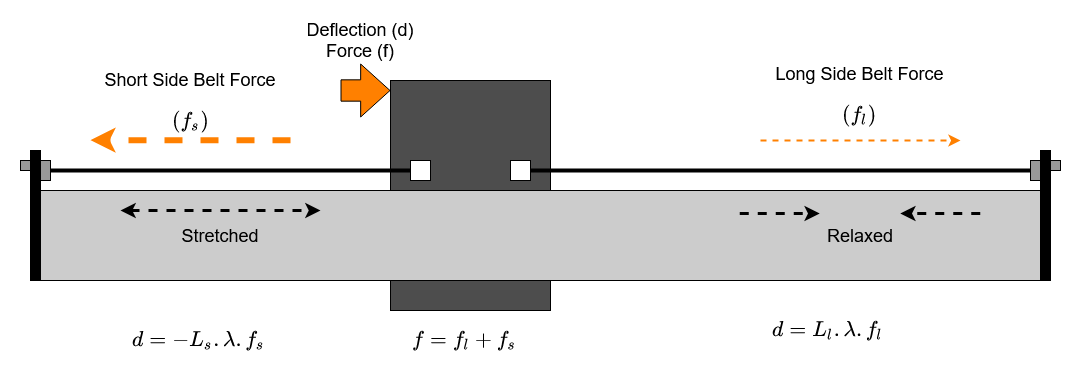
The drive belt system on the Shapeoko relies on belt static tension to work. The belts are tensioned between anchors at each end of the main axis rails. The belt starts with a nominal length and is then stretched to achieve a static tension on the machine. This works because the belt stretches elastically, for each increase in applied force there is a proportional increase in belt length. Note that this is a proportional increase in belt length so a belt twice as long will show half the tension for the same extension. This property of the belt is called the tension modulus and we have a series of measurements of this value for different types of belt. (see the measuring belt tension thread and the measurements by @The_real_janderson ).
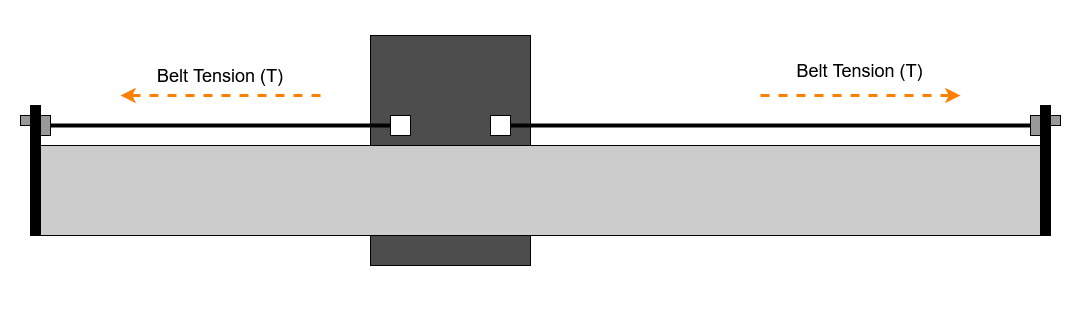
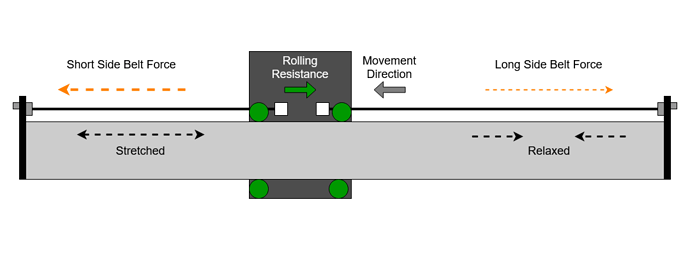
To drive the axis, the belts pass round a set of idler bearings and over a toothed pulley on the drive motor. As the stepper and toothed pulley prevent the belt moving relative to the driven axis, we effectively have two sections of belt. Each is anchored to one side of the moving axis, with the same static tension as the axis is free to move along the rail.
This is the resting state of the belts, equal tension either side of the moving axis, and to satisfy Sir Isaac Newton, no net force on the moving axis, the system in an equilibrium condition.
When we apply an additional force, either by driving the stepper motor to move the axis, or a cutting force from the spindle, the system needs to find a new equilibrium state where all the forces cancel out again. When this happens the belt on one side gets shorter whilst the belt on the other side gets longer.
This results in a net force from the belts which either overcomes friction to move the axis or resists a cutting force. The larger the deflection the greater the force.
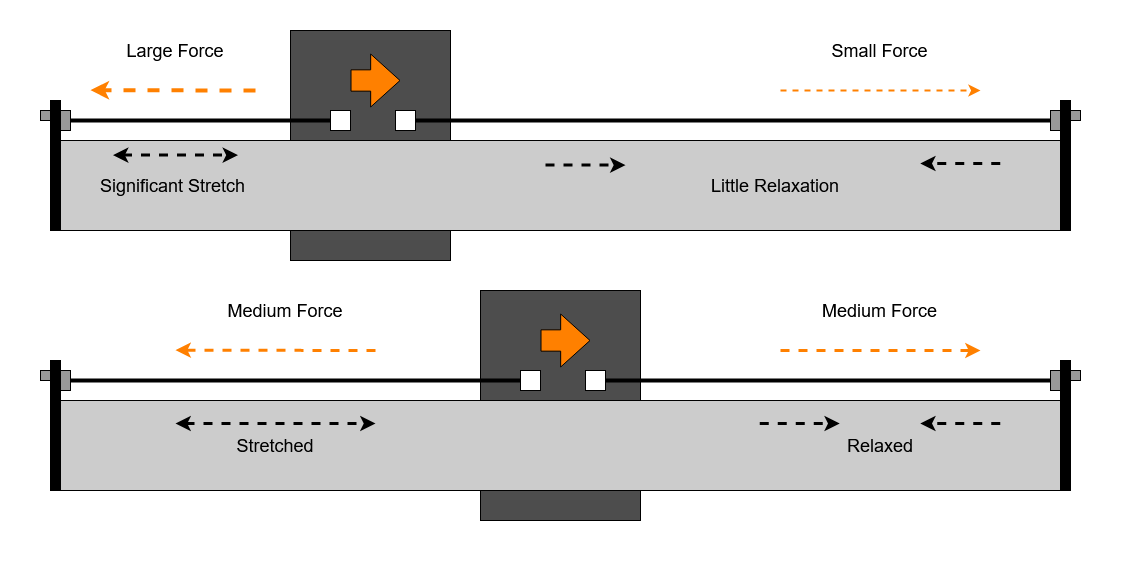
One complication is that, as we know, the stretch of the belt for any given tension is proportional to the length. So for any deflection the longer side of the belt is going to show a smaller change in force and the shorter side a larger change in force. This means that as we get close to either end of the axis the short side belt will produce sufficient restoring force for less deflection distance.
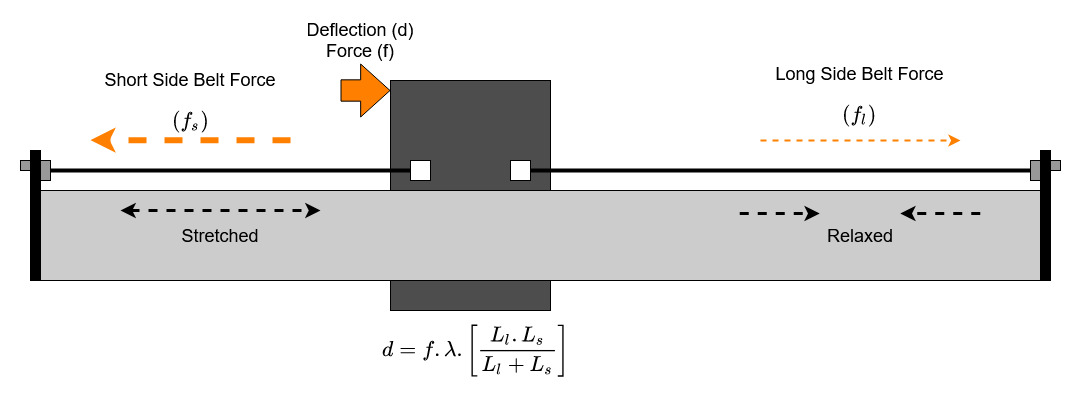
We can easily rearrange to get an equation for deflection in terms of force and belt lengths;
How does the belt drive behave then?
We can use the equations from those diagrams to see what impact all this has on the deflection.
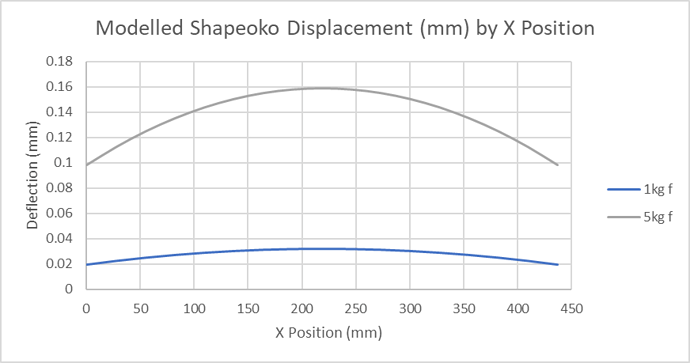
These charts are based on the 9mm Kevlar belts on my machine and the observed tension modulus on the machine. I am seeing ~0.018 % extension per 10 Newtons force. This is lower than that previously measured by the_real_janderson for the Kevlar 9mm belts. This difference may be due to batch variability or rolling friction on the axis reducing the apparent belt tension.
There are a few things we can see from these simplified models;
- The belt deflections are largest in the middle of the axis travel.
- The long axes of the XL and XXL have more belt deflection in their longer belts
- The belt deflection seems to be linear with the applied force on the belts
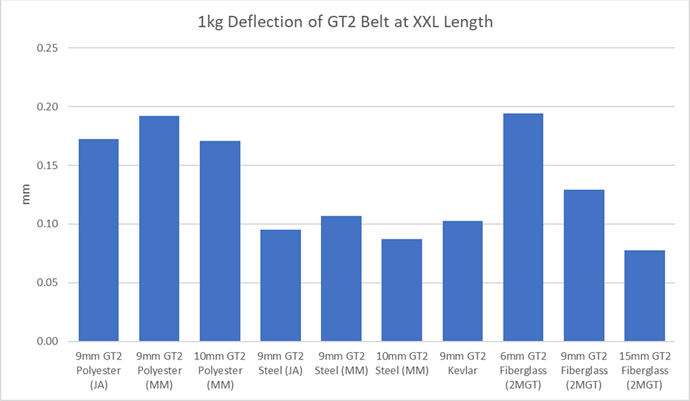
The type of belt in use also has a substantial impact. We have tested or vendor data for a range of belts. Based on that data, this is the belt extension at XXL length and 10 Newtons force
Note the 15mm Fiberglass GT2 which is the type of belt apparently installed on the Shapeoko Pro. This has only slightly better deflection performance than the 9mm GT2 Steel belts, however it does not have the early failure problem when flexed around small radius drive pulleys. The 9mm Aramid / Kevlar belts still appear to be a good option for the non Pro machines.
Axis friction
The other important element in the belt and backlash behaviour, is the axis movement friction.
On my machine it takes between 0.5kg and 1.5kg pull to move the X axis, around double this to move the Y, predictably enough as there are twice as many V Wheels, belts etc. Note that if you measure this, you need to release the belt anchors as there is significant additional movement resistance from the belt and motor system.
When our machine moves it must overcome both the cutting forces and the friction of the moving axis. This results in a certain amount of “wind up” or pretension in the belt to overcome this friction which is what manifests as backlash in the machine.
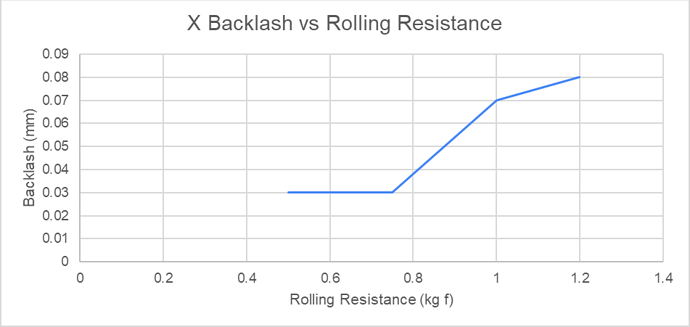
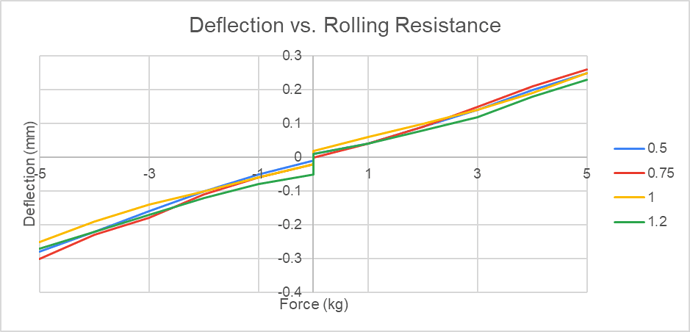
Testing my Z carriage I was able to measure the following behaviour as I increased tension on the V Wheels. This produced a range of rolling resistance and therefore varying backlash
The rolling friction causing backlash is as good a reason as any to not over-tighten your V Wheels.
Slow elastic recovery
One possible source of backlash is if the belts do not immediately elastically recover when the tension force is reduced. This effect is difficult to measure. I performed a simple test to look for this by running the axis into a hard stop and then making the machine take some additional steps to increase belt tension and extension. This was within the belt stretch available from the stepper holding torque. Then I stepped the machine back away from the hard limit to observe whether it took any time to recover to it’s previous step position.
I was unable to observe any evidence of slow recovery within these belts, but this experiment was not particularly well designed.
Size of the error
Taking our measured friction of 10 Newtons we would require, somewhere between 0.02 and 0.2mm of belt deflection to overcome this force, depending upon the axis size, type of belt and how enthusiastically the V wheels are tensioned.
Not just a simple rolling resistance value
I expected this to be a relatively simple rolling resistance from the V Wheels which would give a constant force required to move the axis any distance at any speed. This was not what I observed, and I do not have an effective explanation or model for the behaviour I found.
Testing backlash by reversing direction and moving down from 1mm through 0.25mm to 0.025mm step sizes. At the 1mm step size we see 0.03mm to 0.04mm backlash on this machine, so we would expect to lose an entire step at 0.025mm .
That’s not what happens though, what we seem to have instead is a force required to move the wheels and bearings which depends upon the distance they are being moved. This is presumably some element of plastic deformation as the wheels roll.
The chart shows deflection on the X axis for four different V Wheel tensions. aside from increasing backlash around the zero there is no other significant variation at this measurement accuracy.
Inconsistent Rolling Resistance
One interesting experiment is to disconnect the drive belts and use a weight and pulley to pull the Z carriage along the X axis of the machine. We might expect this fixed force, with just enough weight to overcome the rolling resistance, to smoothly move the Z carriage across the machine.
This is not, however, what happens. As they roll, the V Wheels show significant variation in observed rolling resistance. This varying resistance is likely to affect both precision of movement and backlash by requiring different belt extensions to move at different points on the axis.
(this bit was better explained by the video)
Measurement Time
So, we have some ideas about what is going on but now it’s time to get some real data from the machine. We have a model of the belt behaviour, but for that to be useful it must make testable predictions about the machine.
X Axis Slop, Deflection and Backlash
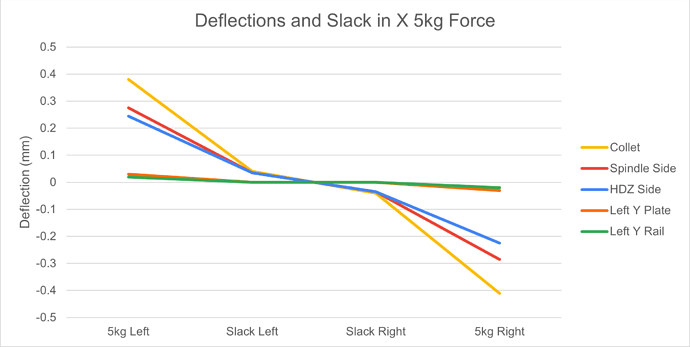
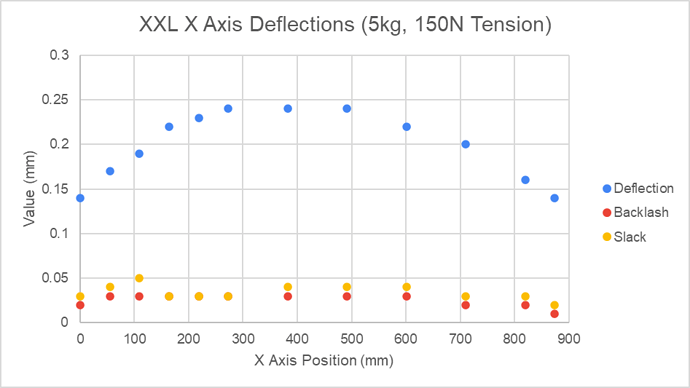
First I measured the X axis slop, deflection and backlash due to the belt system, at 12 different positions across the X axis. To isolate the belt deflection and minimise the contribution of other sources such as the V Wheels, these measurements were made between the X rail and the side of the HDZ close to the X belt. Force was applied to a rod clamped in the collet where the machine would normally see cutting forces. V Wheel tension was set to give just over 10 Newtons of rolling resistance.
To provide a repeatable force, a cord was attached to the rod, and hung over a pulley suspending a 5kg weight. At each location the slack was measured by moving the rod left or right by hand, and observing the distance between where it came to rest when the force was removed in each direction.
Before the deflection measurement, the spindle was moved to the slack position in the same direction as the load to be applied. I did this as I thought it would be less error prone than attempting to set the machine to some notional ‘zero’ position within the slack region. The additional deflection under the 5kg weight was then measured.
Backlash was measured by stepping either left or right in 1mm step mode, reversing direction and observing how much less than 1mm the first direction reversing step recorded. The steps/mm was set to 40.000 on the controller for this test to avoid measurement complication.
The first thing to note is that there is quite a bit of variation in this data, the noise floor appears to be about 0.03mm.
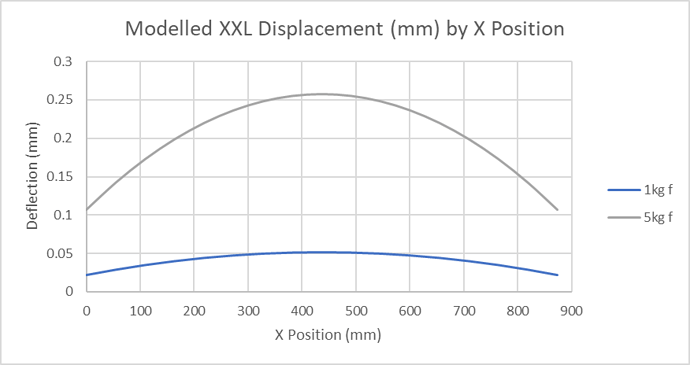
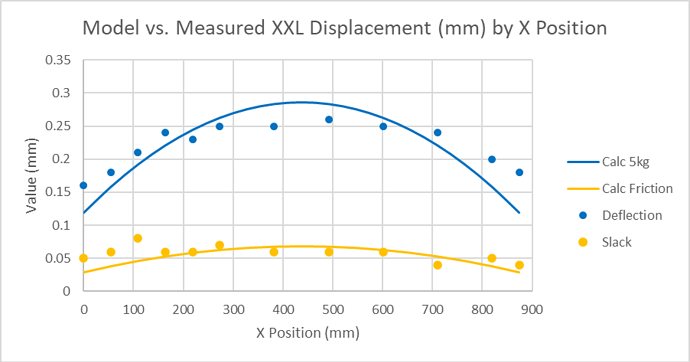
Comparing with the Belt Model
Comparing our measured data with the predicted behaviour from the belt model we have a chart showing;
- The measured slack against the expected belt deflection for 1kg rolling friction
- The measured deflection at 5kg against the expected belt deflection for 50Newton force
The correlation is pretty good given the limits of the test precision and suggests that our model is useful in capturing the basic aspects of backlash and force deflection behaviour in the belts.
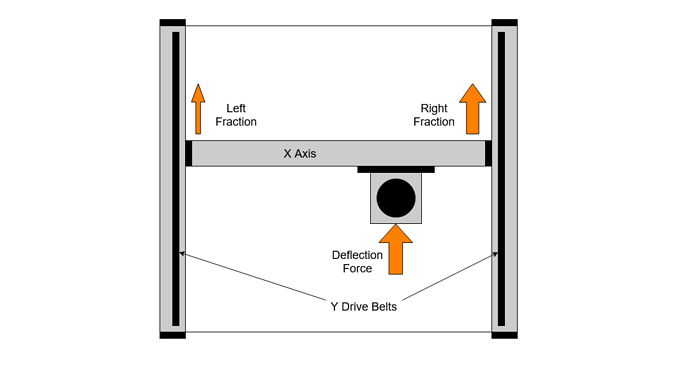
Y Axes’ Drive Belts
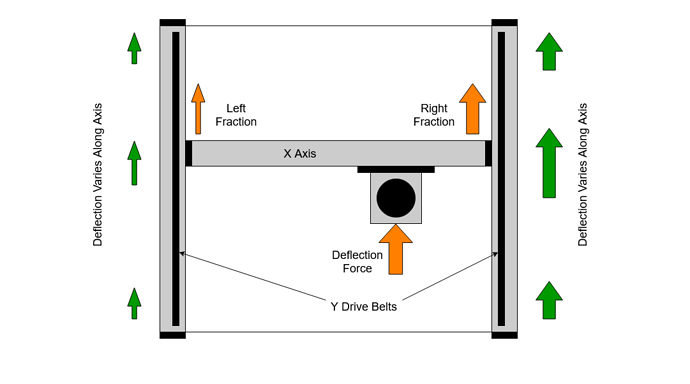
The Y axes are a little more complicated as we have two of them acting together, one at each end of the X axis. This means that the forward / backward forces are split between the two Y axis belts, but in a variable proportion depending upon the X position of the Z carriage.
We can use the same belt deflection model as before, but this time we need to split the force across the two Y axes. We will do this in simple linear proportion as we move left to right on X. We can now calculate the expected deflection for both Y plates for any position of the Z carriage on X
This makes quite clear the variation in forces on the two Y belts and stepper motors as the X position changes. In the middle, we have approximately double belt and motor strength but at each end we drop back down to single.
Using this, we can now calculate the combined effect on the Z carriage position
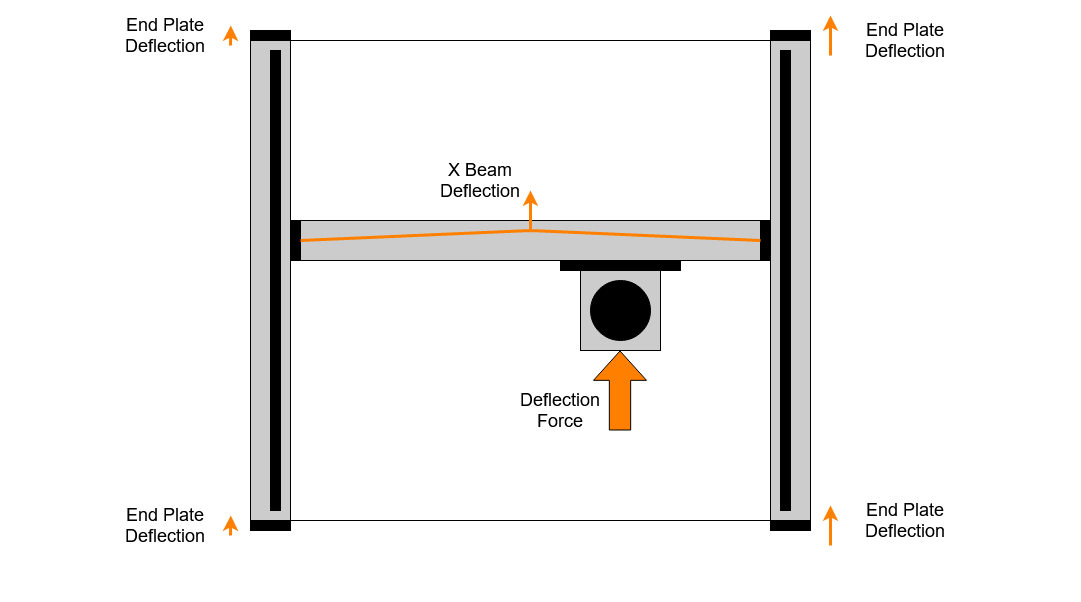
Axis and Steel Plate Deflections
Initial comparison of this model to the measured data showed larger differences than I was expecting or happy to accept, which meant I had to think again about what else might be happening and then take some further measurements. I found that on the XL and XXL the X beam deflection is not negligible, also that the front and rear steel plates were deflecting a measurable amount.
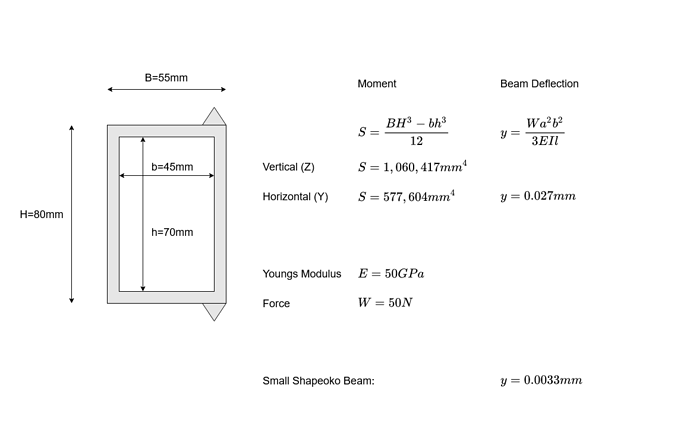
We can calculate the expected deflection of the X beam extrusion using some common engineering maths. We know the Young’s modulus of Aluminium is approximately 70GPa and we can calculate the bending resistance of the beam. We do this using the second moment of inertia, which is based on the cross sectional shape of the beam. Using these numbers and applying a 50N force in the centre of the X beam we get an expected deflection of 0.027mm which is consistent with the ~ 0.05mm peak to peak I measured on my machine.
Notably, if we calculate this for the short X beam of the standard Shapeoko the expected deflection is 0.0033mm, almost ten times smaller.
The deflection of the steel vertical endplates at the front of the machine was also measured and found to be 0.05mm for 50 Newtons, double the peak X beam flex . As we found for the Y belts, this varies with X position as the force distribution alters between left and right.
Model vs. Reality
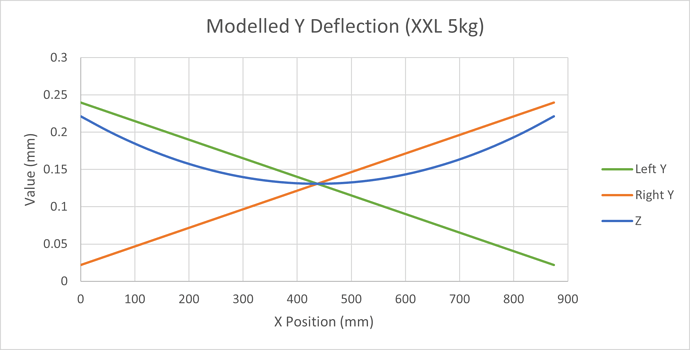
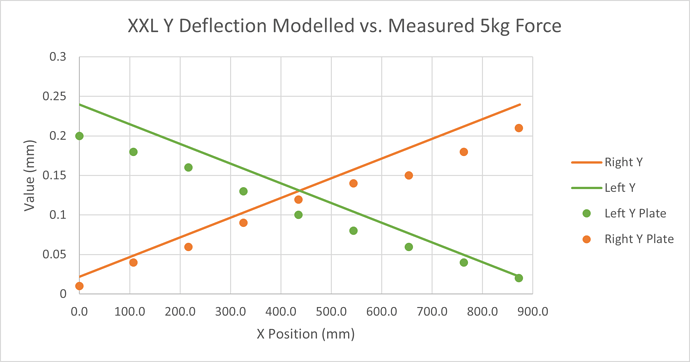
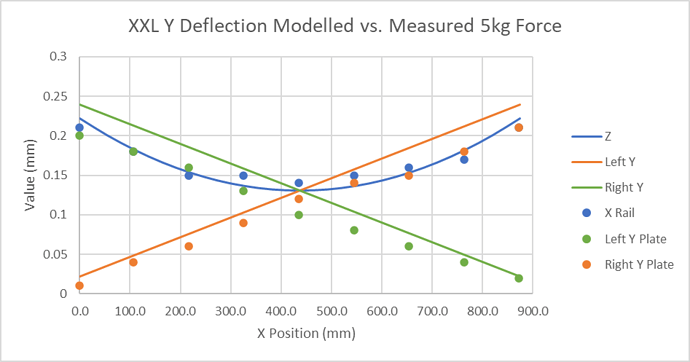
Incorporating the beam and plate deflections and then comparing the new model with the measured data, we have a reasonable alignment of the left and right deflections, with an error increasing as we approach the ends of the X beam
Comparing the Z carriage behaviour we have a pretty good alignment of the modelled and measured data
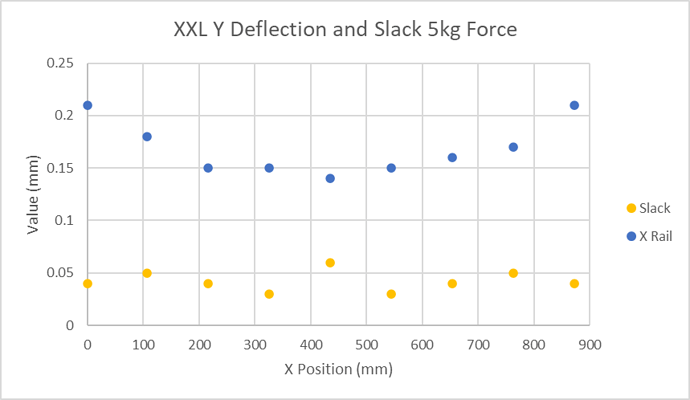
The slack is, as expected, very close to that on the X axis;
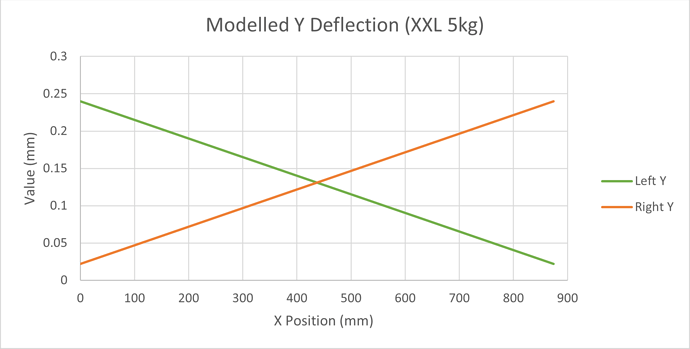
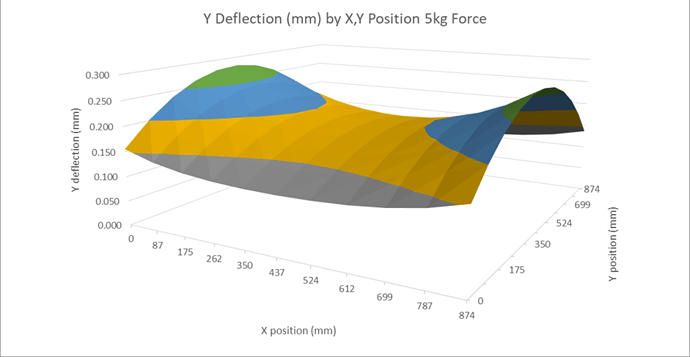
Y Deflection by Position
The Y deflection, as we’ve seen is a bit more complicated than on X. We’ve seen how it varies with X position but, as we already know, the belt deflection will also change as we move along the Y axes. To understand this properly we need to model what happens as the machine travels front to rear as well as left to right. We can use basically the same model we did for the X belt, just applying the appropriate share of force.
Viewing the machine from this direction
We can plot the expected deflection of the Z carriage, in the Y direction like this. The graph is showing the Y deflection in the vertical axis and as colour bands. The surface shows, as the spindle moves around the machine in X and Y and for the same force, how the Y deflection varies.
We can see that the deflections are lowest at the front and back of the machine and worst at the left and right ends of X midway between front and back.
This model is within ± 0.03mm of the measured deflections on my machine so I believe it is a reasonable, if simplified, representation of the major effects.
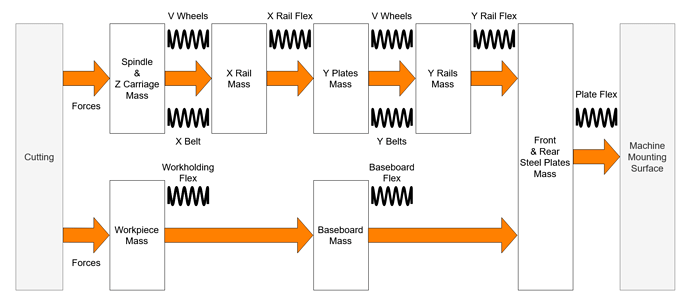
Overall Deflection
Bringing everything together…
We have measured, developed a model, re-measured and made a better model and captured, what I think, are the major elements of deflection. We’ve also seen how various components of the deflection vary as we move in the X and Y axes. It might be interesting to see how this all adds together into the overall deflection of the machine.
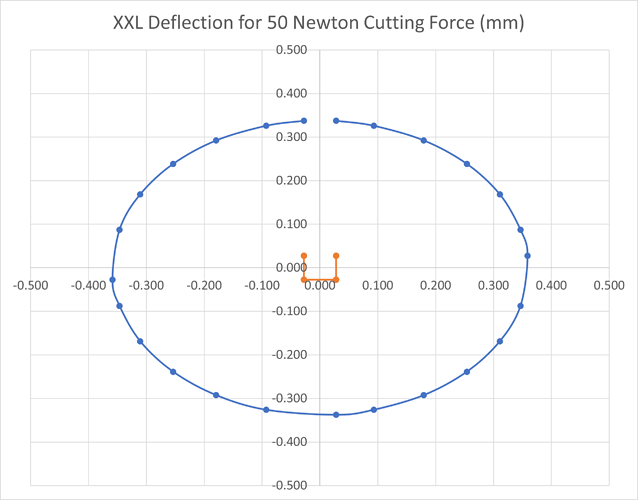
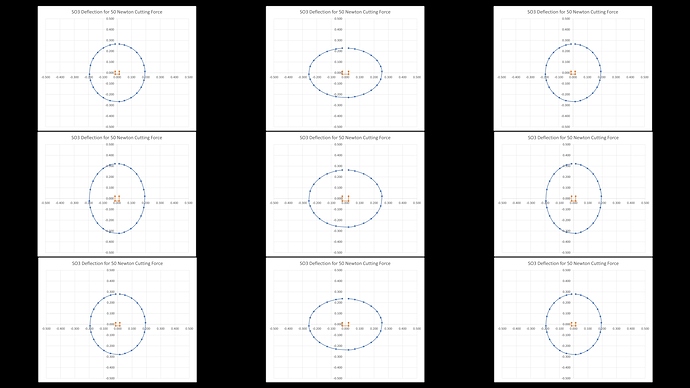
To do this, I’ve used the combined model to plot the resulting deflection for various directions of force on the cutter. The plots show the expected deflection for a 50 Newton cutting force with it’s direction rotated around in 30 degree steps. I apologise for the slightly ugly graphs, but I made them in Excel so that it was easy to share. I’ll post the spreadsheet for anyone who wants to use it.
Remember that we are only plotting deflection in the X, Y plane of the baseboard and not including vertical components such as those seen in the spindle nodding motion.
First we have the plot for the central position on the XXL, the orange box in the middle is the slack and then we see the slightly oval deflection for 50N force in blue, there is a bit more deflection in X than Y in this position.
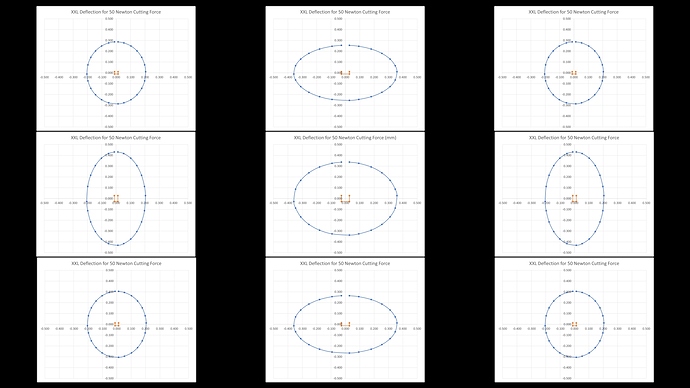
Now for the other positions, the plots are laid out as per the Carbide Motion compass points looking down on top of the machine
On the XXL we can see that the blue deflection plot becomes a lot more oval at the N and S positions as Y deflection reduces as we get close to the ends of those axes. Similarly the W and E become more oval, but this time due to reduced X deflection but increased Y deflection. The four corners are about the same as each other with similar Y deflection to the centre position but reduced X deflection.
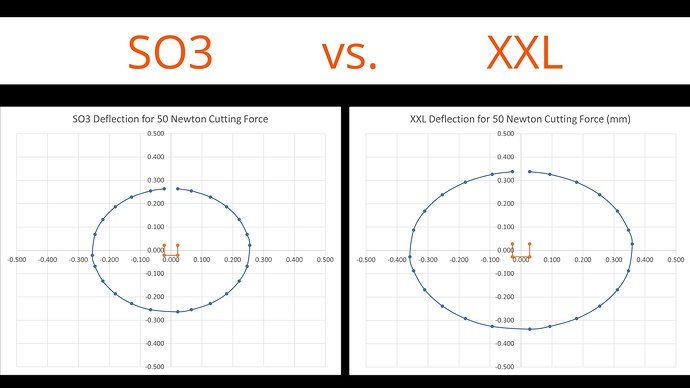
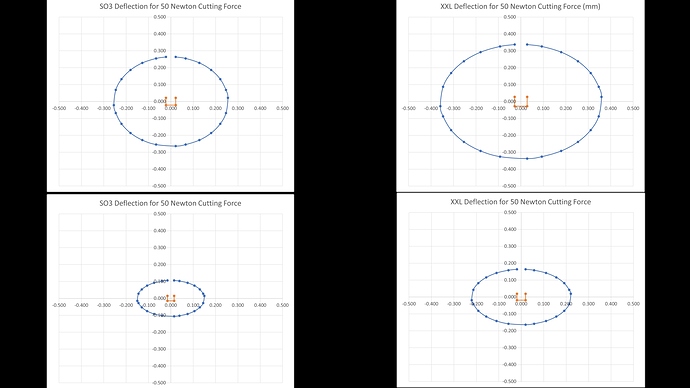
Comparing the SO3 with XXL we can see that the standard machine, despite having the same V Wheels, outperforms the XXL by a significant margin thanks to reduced belt stretch and beam flex. Remember this is not including baseboard bounce. It’s becoming quite easy to see why cuts that are achievable on the standard size machine are more of a challenge on the XL and XXL.
Looking at the rest of the positions for the SO3, we have a similar pattern but with a smaller central deflection oval as well as smaller, better controlled, N, S, W and E plots. Interestingly the four corners are very similar to the XXL despite that machine’s higher deflections toward the middle of the axes.
Upgrades
We can also take a look at what we might achieve with some upgrades, that some of us may already be machining the parts for.
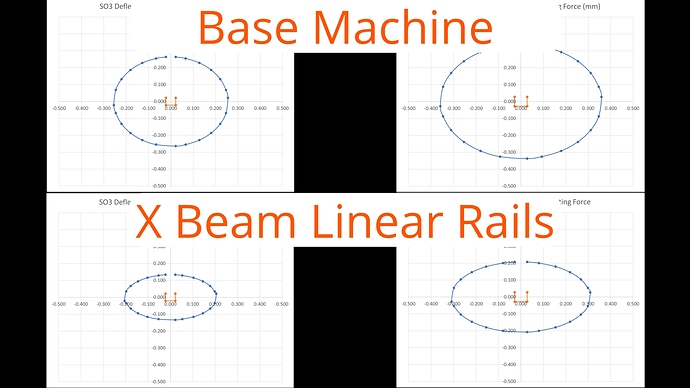
Here’s what the model says about replacing the V Wheels with linear rails on just the X axis. The measured deflections from the Y axis V wheels are much smaller. The change in behaviour is quite significant in both machines, mostly in Y but likely to have quite a strong effect on vibration too as the V Wheel deflections are close to the spindle.
And if we took the next step and upgraded to 15mm wide belts, but with Kevlar or steel core rather than fibreglass we could reduce the belt deflections as well and get something like this
Next Steps
That’s what I’ve got so far, what are the next steps?
- More measurements, clearly

- Proper FEA modelling of the machine to look for the major vibration modes and determine where additional stiffness & damping can help.
- Measure how much of the observed belt deflection is actually coming from stepper motor angular deflection and update the model with this data.
- Properly measure a standard sized SO3 to compare with the XXL and get frame deflections etc.
- Measure an XXL with X beam linear rail upgrade (I will do that soon)
- Measure other belt options installed on the machine